A Mathematical Method for Constructing an Unified Space in Art

Thousand.C. Escher and Tessellations

Feb 01, 2020

Escher's Circle Limit I.

Many of the drawings of Dutch artist Maurits Cornelis (M.C.) Escher closely connect with the mathematical concepts of infinity and contradiction. While these concepts atomic number 82 to many themes, tessellations of the plane appear particularly oftentimes in Escher'south piece of work.

A tessellation (or tiling) of the plane is a construction that fills a apartment surface completely with geometric shapes, usually chosen tiles. Escher often explored symmetric tessellations that were formed by repeatedly duplicating and rearranging only a unmarried tile through translation, rotation and reflection. A simple instance of such a tessellation is one which uses only squares — you lot can imagine the post-obit design repeated to completely embrace an arbitrarily big surface.

Foursquare-based tessellation.

Or, we might have a slightly more circuitous construction using triangles.

Triangle-based tessellation.

From the mathematical perspective, these constructs are oftentimes quite rigid as in the higher up examples, but Escher discovered more complex tessellations that bring visual involvement and aesthetic beauty. This complexity is found in, for example, Escher'due south Lizard.

Escher'south Lizard.

The lizard'southward shape, while on its own not particularly symmetric, combines with copies of itself to create symmetry on a larger scale. Escher uses tessellation to highlight the artistic relationship between positive and negative infinite. In Lizard, at that place isn't a clear distinction between the bailiwick and its groundwork. If you view the lighter-colored lizards every bit the subject, so the negative space is comprised of the darker-colored lizards and vice versa. In a sense, the subject field is its own negative space through the symmetric tiling.

Transformations Betwixt the Rigid and the Organic

Escher'south Liberation.

Escher was probably enlightened of the perceived rigidity of tessellations. In contrast, Escher has a few works in which he depicts the transformation from rigid geometric tilings into organic and natural imagery. Liberation shows a triangular tessellation (similar to the example above) that slowly transforms into an array of birds mid-flight.

Which are being liberated — the birds or the triangles? On the 1 hand, the birds seem to be breaking free from the rigid geometric form of the triangles. But on the other hand, the triangles be in a world of mathematical perfection which has a beauty of its own.

The transformation demonstrates one technique for constructing complex tilings by making small perturbations to an existing tiling. This process is detailed at the end of the post.

Tessellations in Not-Euclidean Geometries

Escher'south Circumvolve Limit III.

Escher's Circle Limit drawings — Circumvolve Limit I is pictured at the outset of this postal service and Circle Limit III is pictured in a higher place — brandish a different kind of tiling than the ones nosotros've talked nigh so far. Up until this point, the tilings nosotros've seen take been such that they could be extended outwards toward infinity on a plane. The Circle Limit drawings instead seem to converge toward a circle. In fact, these are still airplane tilings, but in dissimilar kind of geometry, namely hyperbolic geometry.

In Euclidean geometry, the parallel postulate roughly states: For whatsoever line $L$ and point $P$ not on $50$ , there is exactly one line parallel to $L$ that passes through $P$ . This matches our intuitive notion of parallel lines from our everyday experiences (which Euclidean geometry models). Only it is not necessary for geometry to include the parallel postulate, and hyperbolic geometry is the consequence of modifying the postulate to allow multiple lines to be parallel to $50$ and pass through $P$ .

Taking a look at both Circumvolve Limit I and Circle Limit Iii, both images are based on the Poincaré Hyperbolic Disc. In this model of hyperbolic geometry, we work within a round disk. Lines are represented equally circular arcs that intersect the disc at correct angles. Circle Limit Iii highlights these arcs in the white stripes running along the fish. Two hyperbolic lines are considered parallel every bit long as their arcs don't intersect. Nether this definition, we can confirm that multiple parallel lines can run through the same point — consider the following annotated version of Circle Limit Iii.

Escher's Circle Limit III - annotated.

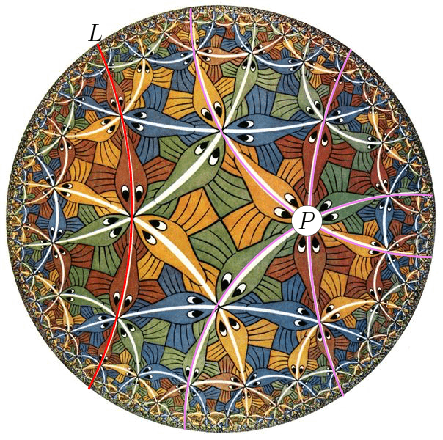
The reddish and pink arcs exemplify lines of this hyperbolic infinite. Telephone call the red line $L$ and the labeled signal where the fish mouths run across $P$ as in the modified parallel postulate. Then, we see that there are indeed multiple lines parallel to $L$ and passing through $P$ past observing the 3 pink arcs passing through $P$ yet not intersecting $Fifty$ .

Interestingly, all the birds in Circumvolve Limit I are the aforementioned size with respect to their hyperbolic geometry, and the same goes for the fish in Circumvolve Limit 3. This is because the notion of measurement in the Poincaré model is different from the notion of measurement in the Euclidean airplane in such a manner that equally spaced objects (from the hyperbolic perspective) are closer to each other (from our eyes' perspective) as you motion toward the perimeter of the disc.

At that place are many other interesting and unintuitive facts that emerge in hyperbolic geometry which you can read more nigh here.

Constructing Tessellations

Desire to create your own tessellation? Ane technique takes inspiration from Escher's Liberation. Start with a simple tessellation (like the geometric examples in a higher place), and make a small modification. Allow'southward start with the square-based one.

Step 1. Outset with a known tessellation.

And and then let's cut out a part of one of the tiles.

Step ii. Modify one of the tiles.

In social club to maintain the symmetry, we must then copy our modification over to the other tiles (making certain to apply the appropriate translations, reflections and rotations).

Step three. Copy the modification to the other tiles.

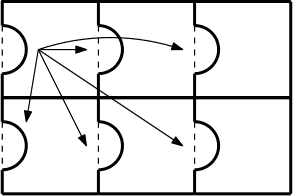
Echo steps ii and three until you lot are satisfied with the result.

Example construction afterwards multiple modifications.

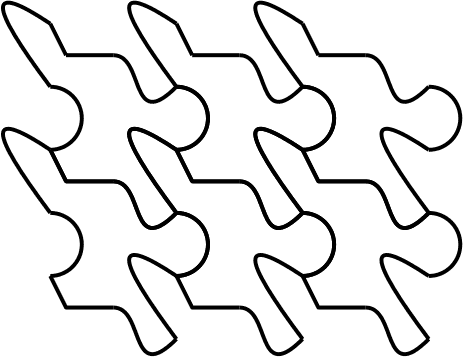
From this process, you tin can arrive at some interesting planar tessellations and gain more appreciation for Escher's art. If you lot're upward for the challenge, yous could endeavor your hand at amalgam a hyperbolic tiling in a similar way.

gillumgodis1985.blogspot.com

Source: https://mathandart.com/blog/escher_and_tessellations/